Institute for Theoretical Physics
			statistical mechanics group| leonardo
This is a copy of the former TINA website. TINA itself is switched off since 27 May 2016 and is no longer available at http://tina.nat.uni-magdeburg . The content has been carefully adapted, media files have been brought up to current standards and some links have been updated or removed. This page now serves as a small reminder of a great project. The penguin is still flying!

Performance

As a first test of Tina's performance we apply the well known Linpack benchmark. Linpack requires the solution of a system of N linear equations with N unknowns. There are several versions the Linpack benchmark, differing in size, numerical precision, and rules.

The reported results have been achieved with gcc 2.95.2.

The 100x100 Linpack

The basic benchmark is the N=100 double precision benchmark, where you are allowed to use whatever compiler optimizations you have at your disposal, but you cannot modify the sourcecode. We used linpackc.c, the C version of the 100x100 Linpack. Compiler options are -DDP -DUNROLL for double precision and loop-unrolling and

for optimization. With that we get 295 Mflops on a single processor.

The 1000x1000 Linpack

As you might have guessed, here N=1000. The major feature of the 1000x1000 Linpack is that you are allowed to modify the source code. All modifications are permitted, as long as your solver returns a result which is correct within the prescribed accuracy. We take the solver from the ATLAS library that comes with Debian. With that we get 460 Mflops for N=1000 and 528 Mflops for N=5000.

Parallel Linpack

This is the benchmark that (hopefully) gets you into the Top 500 list of worlds fastest supercomputers. In the parallel version, you are allowed to modify the source code and to adjust the size of the problem to get optimal performance.

We used HPL, a easy to use parallel Linpack based on MPI.

Fig.1: Parallel Linpack for various problem sizes N and 4, 16 and 64 CPUs.

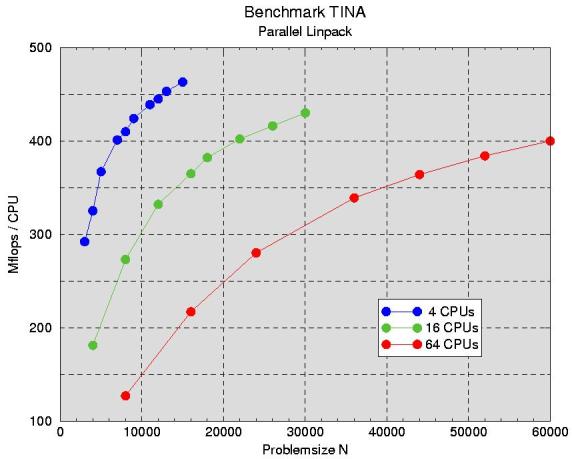The parallel solution of a system of linear equation requires some communication between the processors. To measure the loss of efficiency due this communication, we solved systems of equations of varying size on a varying number of processors. The general rule is: larger N means more work for each CPU and less influence of communication. As you can see from Fig. 1, a 4-CPU setup comes very close to the single CPU peak performance of 528 Mflops. This indicates, that the solver that works in HPL is not significantly worse than ATLAS. The relative speed per CPU decreases with increasing number of CPUs, however.

Fig.2: Parallel Linpack for various memory loads per node.

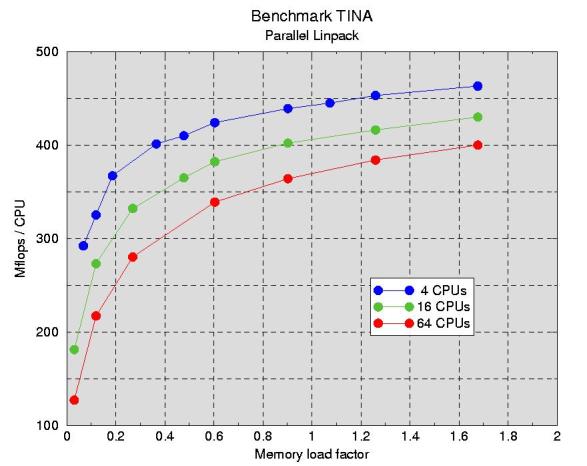The problem size N is limited by the total memory. Tina has 512 MByte per node, i.e. each node can hold at most an 8192x8192 matrix of double precision floats. In practice, the matrix has to be smaller since the system itself needs a bit of memory, too. If both CPUs on a node are operating, the maximum size reduces to 5790x5790 per CPU. To minimize the relative weight of communication, the memory load should be as high as possible on each node. In Fig.2 you can see, how the effective speed increases with increasding load factor. A load factor 1 means that 256 MByte are required on each node to hold the NxN coefficient matrix.

Fig.3: Parallel Linpack on all 144 CPUs.

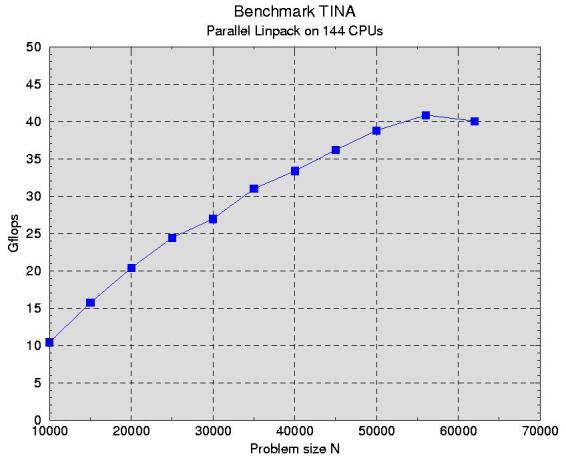With all 144 CPUs, communication becomes the major bottleneck. The current performance of 41 Gflops scales down to 284 Mflops/CPU. The CPUs seem to spend almost half of their time chatting with each other...

We are still working to improve the communication, but the TOP 500 (at least 55 Gflops for the current list, presumably 70 Gflops for the list to come) seems out of reach.

URL: http://tina.cryptoweb.de
Sunday, January 11th 2026, 17:24:31 CET